Quantum and Buddhism Part 2: Experiments 1

This is a continuation of the previous post.
Please read part 1 before this part.

Historically, the Copenhagen Interpretation was the first dominant one in the market until 1952 when Bohm rediscovered de Broglie's pilot-wave theory, which was abandoned in 1927 by de Broglie. Also Born's rule can be considered as one of the earliest interpretation, called the ensemble interpretation.

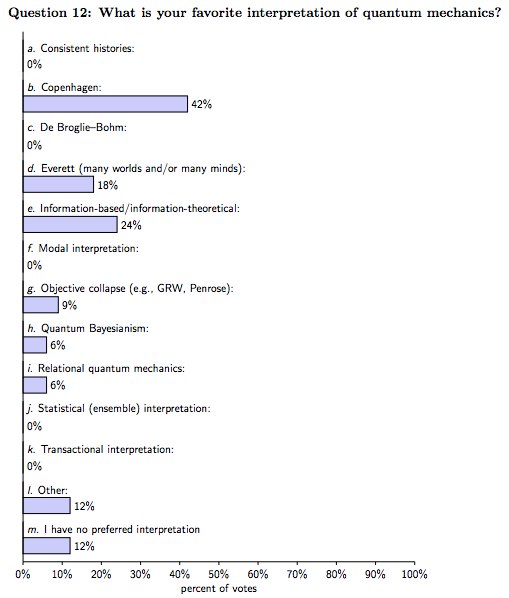
Later on, more and more interpretations flood the market until nowadays we can have popular articles like this: Top 10 favorite interpretations of quantum mechanics. Famous physicist Sean Carroll also put his thoughts in: The Most Embarrassing Graph in Modern Physics.

The table above is not by Sean Carroll, but is the results of a poll carried out among

33 participants of a conference on the foundations of quantum mechanics. The full paper can be read here and it is quite funny. So the main message I want you to absorb here is that there is no consensus on which interpretation is the ultimately correct one. This not comparable to climate change is caused by humans consensus, or vaccines does not cause autism, which are both very well established science with near universal consensus.

It reflects a sad state of popular articles and public knowledge of science when the scientists agree upon climate change is caused by humans and vaccines does not cause autism and the public is more divided in these issues. Yet, when the experts do not agree on how to interpret quantum physics, many many people who write about the topic of quantum usually presents their favorite interpretations as the one true correct one. In particular, the consciousness causes collapse Interpretation and Copenhagen Interpretation are frequently used by many to say quantum physics lend support to Buddhism, without further qualification that these are merely interpretations. We shall see in detail if these interpretation are more compatible with Buddhism or not. But one would be wise not to attach to any interpretation based on your inherent bias before we had done the full analysis.

Here is another graph from the paper. 

Most experts had the humbleness to say that how you choose an interpretations are more of a matter of personal philosophy rather than not.

At this point, it is possible to cringe at any more of headlines of articles that says "Quantum Mechanics proves Buddhism" or the variation of these. It's simply untrue. Quantum mechanics itself is merely a mathematical structure for us to calculate and predict physics, but the story of why it works can be super duper different depending on which interpretation you believe in.

Before going further, here are the description of the remaining experiments from Part 1. The results maybe very surprising to you if you use classical expectations to anticipate the results. This is presented first in hopes of you not using your first interpretations to interpret the results and then be attached to the first one. Just see this as how nature works. We shall revisit these experiments in each of the interpretations later on to give the story of how this particular interpretation make sense of the experiment. For now enjoy the theater show or if you like the magic show, not the backstage or how does the magician does it?

1. Stern–Gerlach experiment

The set up is to shoot silver atoms to an unequal distribution (inhomogeneous) of magnetic field. As suggested by Bohr, angular momentum is quantized. You can think of spin as a form of angular momentum. For those who forgot what angular momentum is, it is mass times velocity time radius of rotation for a massive body rotating around an axis. It can be generalized to everything that rotates has angular momentum. All particles possess this spin property. That's not to say that it physically spin. Silver atoms also has spin. As silver atoms are made up of charged parts, and moving charges generates magnetic fields, all particles made out of charged parts or has charges behave like little magnets (magnetic dipole). And these little magnets should be deflected by the inhomogeneous magnetic field. See this video for a nice classification of what is spin.

Say, if we imagine electrons, protons etc as physically spinning (which I warned is the wrong picture), we would expect that the magnet can point in any direction along the up down axis. To make it more concrete, look at the picture and take the Cartesian coordinates z as the direction in which line 4 points at, the up or down along the screen. y coordinate is the direction from the source of the Silver atoms, 1 to the screen. x coordinate is left and right of the screen then. So the measurement of the spin is now orientated along the z-axis, the up-down axis. If the spin is fully pointing along up or down z direction, it will have maximum deflection as shown on 5. If the spin has y-components, so that it can have a distribution of values between the ups and downs of z axis, then we would expect 4 to be the results of the experiment. This again is the classical picture of thinking of spin as physical rotation, so classical results is 4 on the screen.

Experimentally, the results is always 5. Never any values in between. This might look weird, and indeed is the start of many of the weird concepts we will explore below which is fundamental in the Copenhagen Introduction to quantum mechanics.

Some questions you might want to ask is, do the spins have ups and downs initially (stage one), but they are snap into up or down only via the measurement (stage two)? Or is it something else more tricky?

Stern–Gerlach experiment: Silver atoms travelling through an inhomogeneous magnetic field, and being deflected up or down depending on their spin; (1) furnace, (2) beam of silver atoms, (3) inhomogeneous magnetic field, (4) classically expected result, (5) observed result
Photo by Tatoute - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34095239

Further magical properties is that if I remove the screen, put another inhomogeneous magnetic field pointed along the x-axis (henceforth called a measurement in x-axis) on the beam of atoms which has up z-spin. (The same results happens even if I choose the down z-spin.) Then what I have is two streams pointed left (x+) and right (x-). That's to be expected. If I bring apply again the z-axis measurement onto any of these left or right spins, the results splits again into up and down z-axis.

If you think that this tells us that we cannot assume that the particle remembers its previous spin, then apply another z-axis measurement onto the up z-spin particles, they all go up as shown in the picture below. S-G stands for Stern-Gerlach apparatus, the measurement apparatus which is basically just the inhomogeneous magnetic field. One way to interpret this is that depending on how you measure, measurement changes what is measured.


Picture from Wikipedia

If you put another x-axis measurement as the third measurement on the middle part, one for each beam, the beam which has up x axis (x+) will 100% go up again, and the one with down x axis (x-) will go 100% go down again.

It seems that the rules are

a. Measurement changes the system being measured in quantum mechanics. Only the spin of an object in one direction can be known, and observing the spin in another direction destroys the original information about the spin.

b. The results of the measurement is probabilistic: any individual atom sent into the apparatus have equal chance of going up or down. Unless we already know from previous measurement its spin in the same direction.

This does leads to two things which is troubling to classical thinking. Contextuality, or the answer depends on the question. And inherent randomness. More on contextuality later, for now, we focus on randomness. Normal randomness we have in the classical world is due to insufficient information in the world. If we gather enough data, we can always predict the results of coin toss or dice roll. Yet, in the quantum systems, there seems to be no internal mechanism for them (or is there? Look out for hidden variables interpretation), we have the maximum information from its wavefunction (according to Copenhagen interpretation) and thus the randomness is inherent in nature.

Some people do not like inherent randomness, some do. Why? Classical physics is very much based on Newtonian clockwork view of the universe. With the laws of motion in place, we had discovered also how heat flows, how electromagnetism works, even all the way to how spacetime and mass-energy affect each other in general relativity. One thing is common to all of these. They are deterministic laws. That is if by some magic, we can get all the information in the world at one slice of time (for general relativity, it means one hypersurface), plug it into the classical equations, we can predict all of the past and future to any arbitrary accuracy, without anything left to chance, randomness. That's a worldview of the universe which is deterministic, clockwork, incompatible with anything which has intrinsic, inherent randomness.

So, some view that the main goal of interpretation is to get back into the deterministic way of the universe. Yet, others see this indeterminism as an advantage as it allows for free will. More on that later. For now, let us jump on board to try to save determinism.

If we do not like intrinsic randomness, if we insist that there is some classical way to reproduce this result, then one fun way to think about it is that each particle have its own internal if-then preparations. The particle instructions are: If I encounter the z measurement, I will go up, if x, then I will go left, if z after x, then I will go down, or else I will go up. And so on.

Let's make this more concrete. Imagine if you are a teacher, you have a class of students and you tell them you are going to subject them to a test. The test is a collective fail or success test. The main goal is for the class to behave like the experimental results described. So the students are given time and the materials to study and strategize amongst themselves. Once they are ready, one by one the students come to you, and you will ask many questions of the students, then record their answer. Your question is limited to asking x or z, and the answer is limited to up or down (left and right being relabeled to up or down). That's in direct analogy to the freedom of measuring in the x or z axis and the particles either go up or down.

If you don't like the question being x or z, you can replace it with any yes-no questions with no fixed answer. Eg. Question one is: blue or not? Question two is: red or not? The answers are yes or no. The question does not refer to any specific object being red or blue, but just as an example of questions with only two possible answer but no fixed answer. To preserve close analogy with the experiment, we shall continue to use x, z as questions, up, down as answers. So the "magic" is not in the questions or answers, but in their pattern.

There is no limit to how many questions you can ask any of the students, and part of the student strategy has to take that into account. After the test is done for the whole class and you had recorded their answers, you do the quantum analysis to see if they would obey the rules we found the experiments obey.

Even if one student gives one wrong answer which does not fit into the analysis, the whole class fails. So the students get very serious in their strategy planning. They found that it's simple to win the game or pass the test if they do not have any preconditioned answers to the questions but to just follow the quantum rules, so they ask you if they can decide on the answers on the spot. You detected intrinsic randomness at play here and you come out with rules that the student can or cannot do to satisfy classical thinking requirements. But you do not wish to reveal the true reason you set the rules, so you used the common exam reasons for the rules.

You control which questions you ask without letting them know before hand, you can decide on the spur of the moment too. That's pretty obvious too in the test setting, students who knows what will come out in the exam can score perfectly. The students cannot change their strategy halfway through. That's being unsure of their knowledge. They also cannot decide on the spur of the moment which answers they will give. That's like guessing in the exams. And they cannot communicate with each other once the game started. That's cheating in exams.

Try planning the strategy like the students, if you cannot pass the test, try dropping some of the rules which forbids things. See what kind of rules need to be abandoned to reproduce nature's results.

Here's a sample strategy to get you started.

Student 1: Every time I meet z, I answer up. If I meet x, I answer down. I ignore the order of questioning.

Student 2: Every time I meet z, I answer down. If I meet x, I answer up. I ignore the order of questioning.

Repeat the strategy for each pair of students. It's fairly straightforward to work out that this strategy will fail. The main goal of this exercise is to let you to appreciate the thought experiments physicists have to think when thinking about how to interpret quantum physics, and to see how classical thinking cannot reproduce quantum results.
2. Young's double-slit experiment with electrons

The set up is just to put a traditional double slit in the path of an electron beam, shot out from an electron gun to see if there would be interference in the results or not.

Picture from Wikipedia

Historically, the issue of waves vs particle nature of things started all the way back to Newton. Newton thought that lights are particles, perhaps due to geometrical optics where you can trace the path of light through lenses by just drawing straight lines. There is also a common sense answer (which ignores how small light's wavelengths are) that if light is a wave, how can our shadows be so sharp instead of blurry?

Thomas Young back in 1800s first did the double slit experiment on light. It's basically the same set up as the picture above, just replace the electron gun with a light from a lamp, which is focused via a small hole. Laser hasn't been invented yet then. As light passes through the double slit, if it is made out of particles, we should only see two slits of light at the screen, yet we see an interference pattern!

Wait a minute you might say. You go get a torchlight, cut out two slits out of a cardboard and shine the torchlight through the slits, you see two slits of light shining through. Where is the interference pattern? The caveat for the double slit is that the size of the slit and the distance between the slit should be roughly around the wavelength of whatever waves you wish to pass through it. And the wavelength of light is around 400 to 700 nanometers. For comparison, the size of a bacteria is about 1000 nanometers. The enlarged slits in the picture is merely for illustration purposes, it's not to scale.

What can produce an interference pattern? Waves. Observe the gif below. Waves can meet with each other and if they happen to be in phase at the position where they meet the screen, constructive interference happens, the amplitudes adds up and you see light gathering there. If they happen to have opposite amplitude at another position, destructive interference happens and you are left with a dark region. Destructive interference is also what happens when you use noise cancelling headphones.

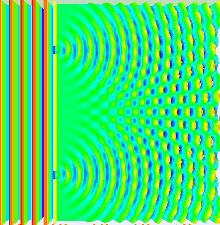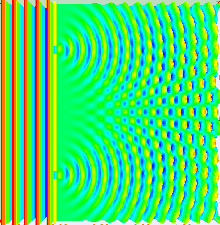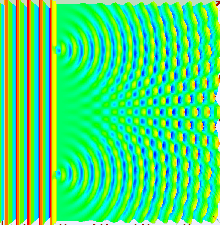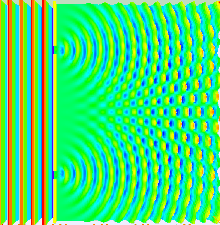
gif from wikipedia

So Thomas Young settled that lights are waves after all, with wavelengths being very small, thus our shadows seems sharp. Next up, Maxwell showed that light are electromagnetic waves with a calculable theoretical speed. Thus it was with great difficulty to accept again that light maybe particles in some other situations. That's why Planck didn't believe the mathematical trick he did had a physical significance. And Einstein was pretty much didn't get much support when he took the idea of photon (light as particles) seriously.

Louis de Broglie had some idea that if waves have particle like properties, might not particles also behaves like waves? It took a long time, but finally, the proper experiment was done using electron beams fired from electron guns towards the double slit only to find (to no one's surprise by then) that yes, electrons exhibit interference pattern too.

What's so hard for classical thinking and expectations to accept is that a thing is either a particle or a wave. How can it exhibit particle like behaviour in some cases and wave behaviour in other cases just for the convenience of explaining what happens in certain cases? Quantum thinking would have to accept a certain relaxation of this criterion that a thing must be either a particle or a wave. So it could be that they have both properties which are real (as advocated by Bohm's interpretation), or that they behave like wave or particles depending on how we set up the experiment (Copenhagen interpretation). Or some other possibilities. It's a common practice to not be too concerned of our language to say it's a particle-wave. Usually we just use the term particle and the wave properties are understood to be there when needed.

Let's take a breath here to reflect that you might not find the results so far as strange at all. I had to point out what kind of thinking (classical) would make these results weird. If you had at all heard that quantum physics upends a lot of classical notions, you would had already come in, prepared to have an open mind and not be attached to classical thinking. So you readily see nothing weird about quantum physics, just a different set of rules. You might be gradually be used to the quantum logic pathway to make sense of quantum, which are called the modal interpretations.

Continuing on the double slit experiments, there are quite a few additions to the basic experiment to exhibit some other properties of quantum systems.

First, the experiment can be done with single particles. Single photon, or single electrons or other particles. Single as in the particles gets shoot through the slit one by one. If it passes the slit, we use a super sensitive detector, capable of detecting one particle at a time and also recording the position of where is the particle detected. Over time, the interference pattern can be seen to be build up again. One by one, the particles somehow knows where to land in order to rebuild that interference pattern.

It gives a creepy feeling for people to think that somehow a single particle has to use its wave properties to feel both slits in order to land at the positions which is consistent with the interference pattern. So a particle can interfere with itself! Different interpretations will give different pictures to this phenomenon. So don't be attached to the first two sentences of this paragraph!

Second variation, we can try to observe which path did the particle took on its way to the screen. There are many subtle details and recent developments in this bit, elaborated more later on when we discuss wave-particle duality.

For now, the simplified version is if we put a measurement device to detect if the particles would go through one slit or another. As long as we can have the information of which path, left slit or right slit was taken by the individual particles as they pass, we see no interference pattern; the particles makes a pattern of two slits on the detector.

For most Buddhists, this is likely not the first time you had heard of this double slit experiment and you might be very eager to see the one thing you are interested from the popular telling of this experiment. The act of observing things (with or without consciousness involved is interpretation dependent) changes what happens to the thing you observe. Do take note that the observation need not necessary involve consciousness and the most important thing is the measuring device is present. Also, we already see this property that measurement changes quantum systems even in the Stern-Gerlach experiment above. Measuring a up spin z-axis particle in x-axis changed its property such that if we measure z-axis after x-axis, the particle can go up spin or down spin in z-axis. The big technical name you can pin to this behaviour can be called contextuality. More technical treatment of contextuality follows later.

Perhaps the most important take away is that do not place all your eggs onto one interpretation yet, just because of preconceived notion that it fits in with Buddhism (we shall see if it does and how it does). Have some patience and open mind to keep on reading and participate in the analysis. As per the spirit of Kalama sutta, there are three main ways of deciding what to believe, revelation, reasoning and experience. The experience part is this section of experiment. The reasoning shall be done in the analysis, revelation is basically all the physics other people had discovered which you are soaking up now. As the experience part is most important in Buddhism, do place the same importance of it in physics. An interpretation of quantum mechanics means it currently has no way to experimentally distinguish itself from other interpretations, or the experiments done to do so had not been thought of yet, or it is not yet technically feasible, or it was done but not universally conclusive and persuasive yet. So no point to attach to one viewpoint (interpretation) based on the notion: it agrees with my view. 

Before going onto experiment no. 3, Bell's inequality violation, we need to settle a number of basic concepts relevant in foundational research of quantum mechanics in order to fully appreciate the importance of that experiment. Historically, before Bell came out with his inequality, these foundational concepts had been largely ignored by physicists. That's because they thought that no experiments could ever probe these foundational issues and they are considered as philosophy work to interpret these rather than physics work. Today, we can distinguish many of the interpretations based on these fundamental properties, three of them will be briefly introduced here. They are locality, counterfactual definiteness and freedom. See the table below for seeing which properties that various interpretations has.

Interpretation	Author(s)	Deterministic?	Wavefunction real?	Unique history?	Hidden variables?	Collapsing wavefunctions?	Observer role?	Local Dynamics?	Counterfactual definiteness?	Universal wavefunction exists?
Ensemble interpretation	Max Born, 1926	Agnostic	No	Yes	Agnostic	No	No	No	No	No
Copenhagen interpretation	Niels Bohr, Werner Heisenberg, 1927	No	No1	Yes	No	Yes2	Causal	No	No	No
de Broglie–Bohm theory	Louis de Broglie, 1927, David Bohm, 1952	Yes	Yes3	Yes4	Yes	Phenomenological	No	No15	Yes	Yes
Quantum logic	Garrett Birkhoff, 1936	Agnostic	Agnostic	Yes5	No	No	Interpretational6	Agnostic	No	No
Time-symmetric theories	Satosi Watanabe, 1955	Yes	Yes	Yes	Yes	No	No	Yes	No	Yes
Many-worlds interpretation	Hugh Everett, 1957	Yes	Yes	No	No	No	No	Yes	Ill-posed	Yes
Consciousness causes collapse	Eugene Wigner, 1961	No	Yes	Yes	No	Yes	Causal	No	No	Yes
Stochastic interpretation	Edward Nelson, 1966	No	No	Yes	Yes14	No	No	No	Yes14	No
Many-minds interpretation	H. Dieter Zeh, 1970	Yes	Yes	No	No	No	Interpretational7	Yes	Ill-posed	Yes
Consistent histories	Robert B. Griffiths, 1984	No	No	No	No	No	No	Yes	No	Yes
Transactional interpretation	John G. Cramer, 1986	Yes	Yes	Yes	No	Yes8	No	No12	Yes	No
Objective collapse theories	Ghirardi–Rimini–Weber, 1986, Penrose interpretation, 1989	No	Yes	Yes	No	Yes	No	No	No	No
Relational interpretation	Carlo Rovelli, 1994	Agnostic	No	Agnostic9	No	Yes10	Intrinsic11	Yes[50]	No	No
QBism	Christopher Fuchs, Ruediger Schack, 2010	No	No16	Agnostic17	No	Yes18	Intrinsic19	Yes	No	No

It is also the (faint) hope of some that as we know more about these fundamental properties and which ones does nature respect, we might be able to rule out some interpretations to finally arrive at the one true interpretation. Indeed, some work had been done to rule out interpretations which has certain combination of these properties. And Bell's theorem is one of the first to do so. A bit of spoiler alert here, Bell's inequality violation means that nature is never simultaneously local (local dynamics in the table) and counterfactual definite. The more common name you might read is Bell's inequality ruled out local realism. As you can verify from the table above, there is no worthwhile interpretation which says yes to both locality and counterfactual definiteness. Unless you consider superdeterminism to be the true interpretation. I will explain what those are as you read on.

We had been talking about classical expectations of how the world should work versus quantum reality of how the world breaks classical expectations. In Bell's inequality, there are three main properties of how the world works are at play.

a. Locality (only nearby things affect each other at most at the speed of light),
b. Counterfactual definiteness, or realism (properties of objects exist before we measure them),
c. Freedom or free will, or no conspiracy or no super determinism (physical possibility of determining settings on measurement devices independently of the internal state of the physical system being measured. In other words, we are free to choose what to measure.)

If the world obeys all these three assumptions, then Bell's inequality cannot be violated. Yet experiments shows that it is violated. Leading us to abandon one or more of these assumptions, depending on one's preference.

We can use the classroom example back in Stern-Gerlach experiment to illustrate the parallels of the restriction rules to the three properties at play here.

In the classroom, each student is allowed to have their own piece of instructions of how to behave when encountering measurement. As quantum measurement can only reveal the probability distribution function after measuring many particles, there might be a need to coordinate what strategy the others will be using. When they are discussing, that's the silver atoms still in the preparation device. As the device activates, one by one the students come out, simulating the silver atoms coming out one by one.

So you as the teacher can in principle choose to have the student go through measurement x or z by asking the questions x or z, and the decision can be made at the spur of the moment. The student coming to the test one by one is parallel to the particles being measured one by one. The questions are measuring devices and having a choice in what to ask allows for freedom and building meaningful results.

The student as they leave their classmates, they cannot communicate with the classmates anymore. You told them it's to avoid cheating in the test, but the real reason is that's the rule of locality. Actually technically it is called the rule of no-signalling. No signalling in quantum setting means no communication faster than light. Why is faster than light relevant here? In principle, the first measurement the first particle (student) encounters does not have to be within the same lab. If we imagine that we have advanced technology, we can allow the particle to travel to the next galaxy, millions of light years away before doing the measurement. So to communicate with the rest of the teammates back on Earth would require faster than light communication.

Another rule is, they cannot change their strategy. Having a strategy means that properties of object exist before we measure them. That's counterfactual definiteness. Counterfactual is what has not happened, like the measurement has not happened, but the properties are definite. There is another common name for this called realism. That's because classical thinking insist upon the moon is there even if I am not watching it. That's pretty close to contextuality. And indeed it is, making the strategy fixed is non-contextuality. Objects answer does not change depending on the question you ask them. Certainly the motion of a ball in free fall does not suddenly change depending on if I ask it what's the velocity or position that that point. And certainly those properties exist before I even ask them. That's classical thinking. Having a strategy and not guessing it means you assume that the student must have the knowledge for the test instead of coming up with the answer on the spur. That's assuming that nature has definite properties even if you do not measure it.

Freedom is your own freedom to ask the questions. That is the experimental physicist freedom to choose which measurement to do first, in which order and to measure which beam. You told the students that if they know what questions will come out, they can cheat in the test. Same thing happens in nature. This is as if the universe is a conspiracy. It will somehow know what you as experimental physicist will choose and adjust so that the right silver atoms (or student) will go to the right experimental measurement at the right time to give the exact right answer so as to reproduce the experimental results. Therefore the alternative name of no conspiracy. In the test analogy, since there is no intrinsic randomness from the students having preset values, and the students already know what you will ask and their order of going for the test can be arranged to present the illusion of randomness to you.

A more scary thought is that if anything (including the universe) can know what you will choose, that means you have no real free will. No free will plus nature is deterministic, means there is nothing that is not fixed from the beginning of time. This is called super-determinism.

Wait a minute, just now we said that nature can choose which atoms to present to you to keep up this conspiracy. Is that not a choice from nature, some sort of free will? Yet, there is no reason for the choice to be made in that instant, it can be fixed from the beginning, since everything can be predicted by nature, or nature already knows, so all possible conspiracy was already fixed back at the start. In that sense, nature also has no real choice. Super-determinism is pretty bad news for science as as Anton Zeilinger has commented:

"We always implicitly assume the freedom of the experimentalist... This fundamental assumption is essential to doing science. If this were not true, then, I suggest, it would make no sense at all to ask nature questions in an experiment, since then nature could determine what our questions are, and that could guide our questions such that we arrive at a false picture of nature."

You might ask for the difference between super determinism vs determinism. Determinism is more of due to cause and effect relationships in the physical equations. Technically for those who uphold the materialism/physicalism philosophy plus determinism, for them, how the mind works is fundamentally due to the physical laws of nature as well, so free will is an illusion. The philosophical technical term for this is hard determinism. Thus there is basically no difference between hard determinism and super determinism for them. For many who believe in true free will but also determinism like the Christians from the days of Newton to the discovery of quantum physics, for them, determinism does not extend to free will, or domain of the soul. The technical philosophy term for this is compatibilism. So there is a difference between determinism of physical phenomenon and super determinism of everything. The Buddhist view on this issue will be discussed later on.

Now let us do the exercise in the first experiment above. Hopefully by now you had some break in between reading from there to here and had some time to think and ruminate on the strategies. Here is a step by step tutorial for that for those who are clueless or too lazy to do the exercise, or those who simply wished to be spoon feed. Just kidding, I think writing this would be my first time analyzing the problem in this framework as well. This is instructive in seeing the underlying reasons for deriving the Bell's inequality, to later see it's violation as something amazing that nature throw at us.

Say we use the sample strategy above and analyse why the teacher would fail the class in that case. When the teacher ask z first then x later, half of the students will give up to z, down to x, another half will give the opposite results. Overall, it seems to be half split into z, half split into x. It only superficially recreate a random result. It also fulfills the first picture below. If the teacher ask those who go up at z, the question z again, the students will give their previous fixed answer to z, the same answer. But grouping the students who give up to question z then seeing that they all go down at question x does not comply with how nature behaves. They are supposed to be half of those who answered up at z to go up at x and another half to go down at x. That's referring to the middle picture below. This strategy cannot also recreate the third picture below.



So the students had thought of all of these consequences and quickly discarded the sample strategy their teacher provided to get them started. They think of partitioning the students more. Partition into four people per group, each group with strategy as follows:

Student 1: answer up at z, up at x.
Student 2: answer down at z, up at x.
Student 3: answer up at z, down at x.
Student 4: answer down at z, down at x.
Ordering of questions does not matter to them.

They can recreate the second picture now while preserving the first picture. Still they fail at the third picture. Those who answer up at z will be students 1 and 3. So the teacher ask only student 1 the question z again. And the results will still only be up. All student 1 in all groups will give the same answer thus the teacher fails them.

Finally, the students gets it. They partition themselves in to groups of four again, with the same basic strategy as above, but here they have to take into account the ordering of questions.

If any questions ask z consecutively, keep answering the same answer as the previous z. Same case as with any consecutive question on x. If there is a switch of the question, say from z to x and back to z, then switch the original answer of z to the opposite of the original value. This holds even regardless of the number of x questions in between the two z questions. Each time there is a switch of questions, switch the answers back and forth. Same case for x, z, x questions.

Confident of their strategy, they rethink what would happen. As before, student 1 is asked z, x, then z again. This time, every student 1 in each group will give down to z. No one answers up. Still not recreating the third picture.

Then they preserve the same ordering rule, but partitioned the students into groups of eight. Any leftovers are welcomed to just fill the last group to however much leftover there is. Statistically the leftovers does not matter as long as we have a lot of groups. If the classroom is not big enough, the students ask the classrooms next class and even the whole school and even neighboring schools to make up the numbers.

The strategy for the first few questions encountered are as in the table below.

	Questions
Students	z	x	The z after the first switch of z, x, z
1	up	up	up
2	up	up	down
3	up	down	up
4	up	down	down
5	down	up	up
6	down	up	down
7	down	down	up
8	down	down	down

Now the ordering rule reads, switch the latest answer of z to its opposite for subsequent switching of questions.

Now they think if the teacher ask only three questions maximum to each students, the teacher cannot detect any difference statistically from the quantum results. Unless, another student points out, the teacher ask x, z, x.

Face-palming themselves after inviting so many students from neighboring schools and yet still fail to come out with the winning strategy, the clever ones just try an update to groups of 16. This time, the x, z, x ordering are taken into account and the ordering rule also updates to the same for them, switch the latest answer of z or x to its opposite for subsequent switching of questions.

	Questions
Students	z	x	The z after the first switch of z, x, z	The first x after switching from x,z,x
1	up	up	up	up
2	up	up	up	down
3	up	up	down	up
4	up	up	down	down
5	up	down	up	up
6	up	down	up	down
7	up	down	down	up
8	up	down	down	down
9	down	up	up	up
10	down	up	up	down
11	down	up	down	up
12	down	up	down	down
13	down	down	up	up
14	down	down	up	down
15	down	down	down	up
16	down	down	down	down

Now as the group grows bigger, the number of clever students also increases. Another clever one pointed out that the teacher can ask more than three questions per student. We will fail then. The original group who thought of the ordering rule said that the ordering rule should take care of it.

"Really?" challenged the clever student. They rethink about it.

Say the teacher ask z,x,z,x,z,x. Six questions in that order.
The answer for each of the students are clear from the rules above. Following student 9, the teacher would get the following answer: down, up, up, up, down, down. The last two are due to the ordering rule.

The following table shows the results that the teacher would collect. The teacher happens to group the same answer to the same label, which she happen to label the same label as the student's strategy. One of the student quick with Microsoft Excel made a quick table.

	Questions in order
Students	z	x	z	x	z	x
1	up	up	up	up	down	down
2	up	up	up	down	down	up
3	up	up	down	up	up	down
4	up	up	down	down	up	up
5	up	down	up	up	down	down
6	up	down	up	down	down	up
7	up	down	down	up	up	down
8	up	down	down	down	up	up
9	down	up	up	up	down	down
10	down	up	up	down	down	up
11	down	up	down	up	up	down
12	down	up	down	down	up	up
13	down	down	up	up	down	down
14	down	down	up	down	down	up
15	down	down	down	up	up	down
16	down	down	down	down	up	up

Compare it to the quantum results. For the quantum results, we collect all measurement of which the silver atoms goes down at the first z, up at the next x, up at the next z, up at the next x, then put z again to that value, we expect to see the beam to go half up, half down as the previous x measurement erased the memory of the up at the previous z.

The only students which would satisfy this selection is students with strategy of student no 9. Yet, all student 9 will give only one answer to the subsequent z measurement. Down.

At this point of the analysis, the students realize that they would need to continually double the size of the group to the maximum amount of questions the teacher can ask. We doubled from one student four times (two to the power of four) to get 16, and it can only fit to the quantum case for up to four questions. Since the teacher told them that there is no limit to the amount of questions that she can ask, they need an infinite amount of students to have infinitely long strategy to win all the time.

Throwing their hands in the air, they cried foul to the teacher and explained their findings.

Now putting yourself back as the teacher, you look to see the analogy with the silver atoms. You ask yourself how many measurements of alternative switch do you need to do on the silver atoms to completely verify that there is no classical strategy like above to reproduce the experiment? A quick guide in the amount of silver atoms there are in 108 g of silver, the weight of one mole of silver is the avogadro's number, that is 6.02*10^23. How many doubling of twos is that number? It's 79. 2^79 would just be slightly bigger than avogradro's number. So just do the alternate measurements eighty times, if you plan to use up all 108g of silver in the Stern-Gerlach experiment to completely verify that there is no way nature can conspire with such strategy.

Now I am not aware that any experimentalist had done this yet, but it's a good paper to write if you are one and happen to have all the equipment at hand! Of course this will be very technically challenging as it entails measuring to about one or two atoms of silver at the last few stages of measurement. Not to mention all the losses that would occur at the process of heating up the atoms to become a beam, controlling the beam to be one atom at a time, doing in in vacuum to avoid air pushing the silver atoms out of the path and so on.

Suffice to say that theoretically speaking, we must abandon one of the rules which we had set up previously for the students to pass the test. To choose which rules to abandon and the subsequent strategy which the students are free to employ are part of the work of interpretation of quantum. Nature is not classical, but just how not classical it needs to be? In particular, which part of classical should nature abandon to behave like quantum? You might also read somewhere else that says the same thing in different words: Just how weird quantum needs to be? Which weirdness are you comfortable with? That's pretty much how people choose their interpretations.

So knowing that different students in the class will have different preferences for which weirdness they are comfortable with, you divided the class into three unequal groups. One is allowed to break locality, the second allowed to break counterfactual definiteness and the third allowed to break freedom. You explain a bit of what these concepts are and which rules the tie in to and let the students pick their own group. I am skipping contextuality here as it is more clear to do that in another kind of inequality. Also technically this case is not the experiment studied by the Bell's inequality violation, so it's more of a tutorial case for you to get familiar with how physicists do fundamental quantum research.

Once the sorting is done, each group works out their solution to your test, taking full advantage of the one rule they can break. Let us visit them brainstorming one by one. Don't worry, the workings are much shorter than what we had done above.

1. Locality violation, or Non-locality.
   
   This allows the student coming up to communicate with the rest of the classmates as he answers the questions. He can tell the rest what questions he received, but it's not useful as it's not guaranteed that the teacher will use the same ordering of questions on the next person. He can communicate how many questions he got in total, but it's again not useful as the teacher can always increase the number of questions for the next person. He can tell the classmates what he answered, but everyone already know what he will answer to all possible combination of answers if the strategy is long enough. Overall, relaxing this rule does not help.
   
   This is perhaps not so surprising as back in 1922, when the Stern-Gerlach experiment was performed, no one was concerned about locality violation from this experiment. We need minimum of two particles and two measurements to possibly test for locality violation. That's what the Bell's inequality violation experiment uses. It's called quantum entangled particles.
   
   
2. Counterfactual definiteness violation, or no fixed answers, or answers does not exist before we ask the questions.
   
   This allows the student to go out with just a small list of instructions, like a computer programme, which can easily replicate quantum results. The instructions are as follows. Each student has only to remember two bits of information, or in colloquial terms, two things. That is there are two memory slots, each capable of storing one of two states. In computer language, it would be 0 or 1. We can relabel them to any two valued labels like x or z, up or down.
   
   When they go for the test both memory slots are empty. The teacher ask the question of either x or z. The student stored the questions ask in the first slot. The answer the student gives depends on a few factors.
   
   If the first slot was empty before hand and just got a new value, and the second slot is also empty, the answer is a random selection of 50% chance up or 50% chance down. Store the answer in the second slot memory.
   If the first slot was not empty, compare the question to the first slot. If the question is the same, use the same answer in the second slot memory. This ensures that if the teacher ask z, z in a row, the second z will get the same answer as the first z.
   
   If the question is different from the first slot, discard the second memory and do the random selection again and store the new value in the second slot memory. Also, update the first slot to the latest question.
   
   Example. The student comes up, got the question x. He randomly selects up as the answer. The next question is x. He gives the same answer up. The next question is z, he forgets about question x, updates his first slot with z, selects random results, say down and also updates the second slot. The next question is x, he updates the first slot with x, select random results, say down and updates the second slot with the new answer. And so on.
   
   That's all that is needed to replicate quantum results. The crucial freedom here is that the answers do not have to exist before the question is asked. And if no question is asked, eg. on consecutive questioning of z, z, there is no meaning to ask if the teacher had asked x instead of z as the second question, what would the answer be? Since x was not asked on the second question, it is counterfactual, and there is no definite answer to that question.
   
   This way, each student can have a finite, small list of instructions on what to do for all questions, so the number of questions asks does not matter. The number of students required does not matter as the strategy does not depend on that. Well, as long as it's enough to do a statistical analysis. Students can pass the test with 100% certainty.
   
   Contextuality is not really apparent here and is better tested via other means.
3. Freedom violation, or cheat mode enabled.
   
   It's a bit tricky to detail how the students can win with this. It entails placing restrictions. So the students know before hand that the teacher cannot possibly ask infinite amount of questions. They already know the maximum amount of questions which the teacher will come out with. It's never infinity. And they can know which sets of questions the teacher will ask for the first student and second one and so on. They can then arrange for the student who prepared their strategy just up to the maximum amount of questions the teacher will ask that student to.
   
   Eg. if the teacher will ask 10 questions to the first student, the first student who goes out only needs to prepare until 10 possibilities. Normally, the students also do not know which x, z ordering of the questions will come out and the student has to prepare their answer for 2^10, or 1024 possible sets of questions. One set can read all 10 x, another can be x,z alternate, another can be z, x, x, z, x, x, z, x, z, x. Each questions can have 2^10 possible answers too. Like all 10 ups, or up, up, down, down, up, down, up, up, up, up. So it's 1,048,576 possible answers.
   
   We simplified the possibilities in the analysis before relaxing the rules by using for all question x, answer up etc. It selects a narrow range from all these possibilities, with the advantage that the student can have fixed answers up to infinite questions. Also the quantum results already ruled out most of the possible answers. Like for consecutive x, x, we can only have either up, up or down, down, not up, down or down, up. That's half of possible results gone with one of the quantum rules. We just have to replicate that by ruling out impossible results.
   
   But now, we know exactly which of the 1024 sets of question ordering the teacher will ask, as this is a conspiracy. So we only need to prepare the first student for a minor selection of the 1024 possible answers left to give to be consistent with quantum results. We can also prepare all others to fit in with the first student to get a quantum statistics overall, tricking the teacher.
   
   There is just one tiny detail left to address. The teacher also selects the amount of students. So what if the teacher asks more questions than there is enough students to answer to provide the quantum statistics for? Then it's the fault of the teacher for not allowing enough students to participate or asking too many questions. The teacher cannot conclude anything without enough data.

Wait, this last bit of information does seemingly destroy our reasoning that nature is not classical above. There is no point doing 80 measurements of alternative directions if we do not provide more than one mole of Silver atoms to get the statistics. Adding up more silver atoms allows for nature to cheat on us. Not adding means we do not have enough data to conclude that nature can be fundamentally classical.

The solution to this conundrum is to realise that to be paranoid about nature betraying us is actually assuming the conspiracy theory. Look at the word cheat on us in the previous paragraph. If nature is fair and classical, we should already gotten deviation from quantum results way before having to do 80 measurements in a row. Which is probably why no one bothered to do this experiment. If nature cheats on us anyway, there is no way we can ever know. That makes the last assumption, no freedom, or super-determinism fall into the category of unfalsifiable interpretation.

Now, satisfied with the results of our analysis, most people conclude that nature is counterfactual indeterminate as you can imagine super-determinism is not popular with people. Historically, super-determinism is not considered until Bell's inequality is shown to be violated. Thus, it would be interesting to explore how does some of the interpretations can still retain counterfactual definiteness. We will discuss their explanation of these experiments when we get to them.

So many people are quite comfortable to say quantum experiments tells us that nature does not exist until you observe them from throwing out counterfactual definiteness, or realism. Yet, this is deliberately excluding those interpretation which still retains realism. Strange, is it not, that even this seemingly fundamental part of what almost everyone thinks what quantum is turns out to be not necessarily true.

Next up, we will talk more on Locality and Bell's inequality violation in Part 3: Experiments 2.